本文主要介绍大名鼎鼎的“word2vec”。word2vec顾名思义,就是将词表示为一个向量,表示出的向量可以运用在各种各样的任务上。可以说,在BERT等模型诞生前,这个词向量的表示方法是最为流行的方法之一。
本文主要包括:
- Onehot vs 分布式表示
- CBOW和skip gram
- Huffman改进
- 负采样
为什么要分布式表示
在做NLP的时候,对于词最简单的处理方法就是对词编号,然后把每个词表示为One-hot向量。更具体的说,给定V个词,我们可以按照字典序进行排序,下标0~V-1对应着每个不同的词。而One-hot向量一个\(V \times 1\)维的向量,对于下标为a的词,其的向量中下标a为1,其余均为0。
可以看出,One-hot向量的维度和词库的大小成正比,得到的是十分稀疏的向量(因为只有一个位置为1,其余都为0)。
此外,这种One-hot的向量表示几乎没有表达语义信息的能力。因为任何两个词之间都是正交的,我们常常使用的余弦距离结果都是0,这也与实际情况不相符,往往我们会有近义词、反义词等关系。
因此,就要让我们今天的主角word2vec来解决这些问题啦~
word2vec是一种词的embedding方法,在介绍之前,首先了解一下啥叫embedding呢?
参考知乎用户寒蝉鸣泣的解答:
Embedding在数学上表示一个mapping, f: X -> Y, 也就是一个function,其中该函数是injective(就是我们所说的单射函数,每个Y只有唯一的X对应,反之亦然)和structure-preserving (结构保存,比如在X所属的空间上X1 < X2,那么映射后在Y所属空间上同理 Y1 < Y2)。那么对于word embedding,就是将单词word映射到另外一个空间,其中这个映射具有injective和structure-preserving的特点。
通俗的翻译可以认为是单词嵌入,就是把X所属空间的单词映射为到Y空间的多维向量,那么该多维向量相当于嵌入到Y所属空间中,一个萝卜一个坑。
word embedding,就是找到一个映射或者函数,生成在一个新的空间上的表达,该表达就是word representation。
在Word2vec中,每个词向量都会表示为K维的稠密向量,这样一来,达到了降维的效果。此外,word2vec假设具有相同上下文的词语包含相似的语义,使得学习到的词向量映射到欧式空间后有较高的余弦相似度,更符合实际的表示。
Fake Task
我们想要得到的是词的向量,而在训练word2vec的时候,其实目标并不是得到词的向量,词的向量其实只是学习到的“副产品”。
那么目标是什么呢?真正训练的目标是:给定一个词,计算当这个词出现时,它临近的其它词出现的概率。这里的“临近”指的是设置一个窗口大小,比如将窗口大小设置为2,意味着该词的前2个和后2个单词会纳入训练样本中,下图就是一个例子:
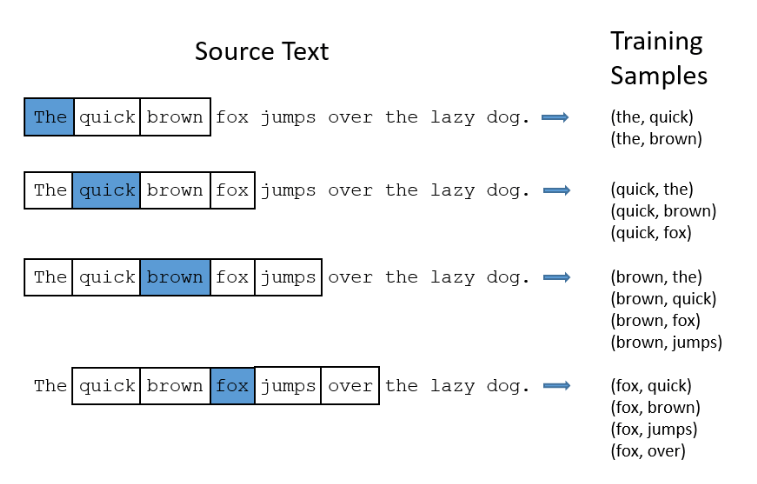
比如fox出现的时候,我们想知道quick词出现的概率。
我们把给定的词称为“中心词”,临近词称为“背景词”。比如上图最后一个例子,fox为中心词,而比如quick等词就称为背景词。
这种给定中心词计算背景词的方法称为Skip-Gram模型, 假设给定中心词的情况下背景词独立,上图最后一个例子可以用条件概率表示为: \[ P(\textrm{quick},\textrm{brown},\textrm{jumps},\textrm{over}\mid\textrm{fox}) = P(\textrm{quick}\mid\textrm{fox})\cdot P(\textrm{brown}\mid\textrm{fox})\cdot P(\textrm{jumps}\mid\textrm{fox})\cdot P(\textrm{over}\mid\textrm{fox}) \] 还有另外一种给定临近词计算中心词概率的方法,称为CBOW模型,同样可以用条件概率表示为: \[ P(\textrm{fox} \mid\textrm{quick},\textrm{brown},\textrm{jumps},\textrm{over}) \] 可以先记住下面很直观的图(左边为CBOW,右边为Skip-Gram):
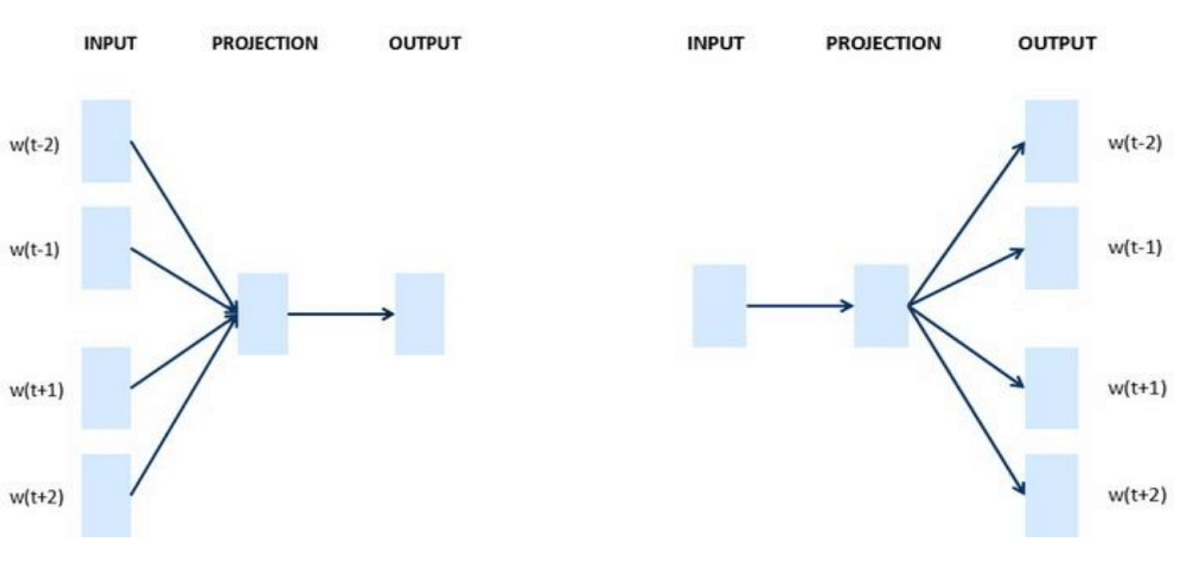
下面就详细的介绍这两个算法。
Skip-Gram
上面提到,Skip-Gram是用中心词去预测背景词的。给定长度为T的文本序列,窗口大小为m,上述所说的预测概率过程可用极大似然估计表示为: \[ \prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(w^{(t+j)} \mid w^{(t)})\tag{3-1} \] 而该目标与最小化负对数似然函数等价: \[ - \sum_{t=1}^{T} \sum_{-m \leq j \leq m,\ j \neq 0} \text{log}\, P(w^{(t+j)} \mid w^{(t)})\tag{3-2} \]
要是知道概率P的形式,我们可以用梯度下降的方式进行训练,那么概率P是什么呢?先来看看Skip-Gram的网络结构:
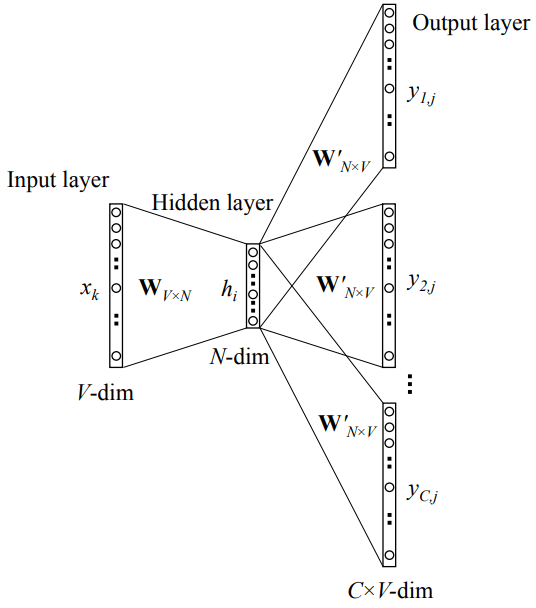
这是一层的神经网络,输入是one-hot后的向量\(\bf x\)。假设词库大小为V,对该中心词进行编号,如果该词编号为k,则\(x_k = 1\),其它位置都为0,维度为\(V \times 1\)。
然后是矩阵\(\bf W\),维度为\(V \times N\),则输入到隐层的操作其实是矩阵的相乘,\({\bf v_k} = {\bf W^T x} = {\bf W_k^T}\), 即相乘后其实得到的是矩阵\(\bf W^T\)中的第k列(称为\(\bf v_k\)),其维度为\(N \times 1\)。
从隐层到输出层则是另一个矩阵\(\bf W'\),这个矩阵维度为\(N \times V\),设\(t_{c,j} = {\bf v_k^T u_j }\),其中\({\bf u_j}\)为\(\bf W'\)的第j列(\(N \times 1\)),结果得到一个数\(u_{c,j}\)。这里\(u_{c,j}\)代表输出的第c个面板的第j个单词的值(因为要输出C个结果)。然后我们可以放入Softmax进行概率归一化: \[ p(w_{c,j} = w_{O,c}|w_I) = \hat{y}_{c,j} = \frac{\exp(t_{c,j})}{\sum_{a=1}^{V} \exp(t_{c,a})}\tag{3-3} \] 其中,\(w_{c,j}\)为第c个背景词输出向量的第j个单词的值,而\(w_{O,c}\)为背景词中的第c个单词,\(w_I\)为输入的单词。合起来就是说给定单词\(w_I\),第c个背景词为第j个词的概率。
但其实隐层到输出层的权重矩阵\(\bf W'\)是共享的,\(t_j = t_{c,j} = {\bf v_k^Tu_j }\),因此可以看成C个背景词分别进行前向传播, 模型简化如下:
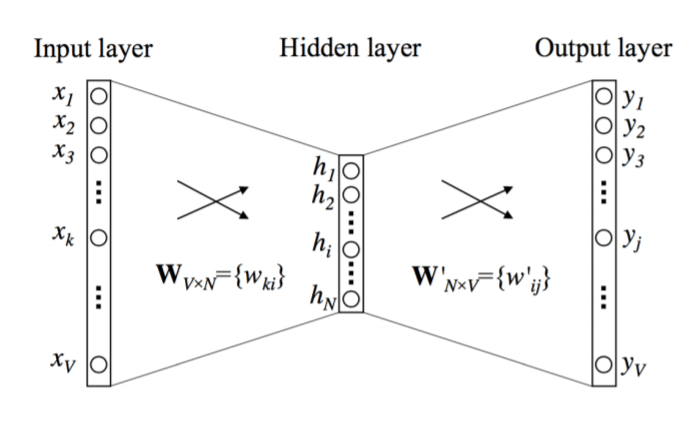
公式也可以简化为: \[ p(w_j|w_i) =\frac{\exp(t_{j})}{\sum_{a=1}^{V} \exp(t_k)} = \frac{\exp({\bf v_i^T u_j})}{\sum_{a=1}^{V} \exp({\bf v_i^T u_a})} \tag{3-4} \]
注意到\(\bf v_i\)和\(\bf u_j\)是两个词\(w_i\)和和\(w_j\)的词向量,前者来自矩阵\(\bf W\), 后者来自矩阵\(\bf W'\)。
因此,对于skip-gram模型来说,计算 \(P(\textrm{quick}\mid\textrm{fox})\) 时输入的为fox的one-hot向量,y则为quick单词one-hot向量,其它的\(P(\textrm{jumps}\mid\textrm{fox})\), \(P(\textrm{over}\mid\textrm{fox})\)同理。这样就相当于计算了共现的概率,可以用反向传播来学习。
学习结束后,可以选择\(\bf W\)或者矩阵\(\bf W'\)作为我们的词向量矩阵,比如选择\(\bf W'\),则每一列就是我们对应单词的embedding后的结果。
训练
假设我们采用随机梯度下降进行训练,即每次只选取一个中心词(假设编号为i)来计算梯度,则损失函数为:
\[ \mathcal{L} = -\sum_{-m \leq j \leq m,\ j \neq 0} \text{log}\, P(w^{(i+j)} \mid w^{(i)})\tag{3-5} \]
这里首先对式3-4取对数为: \[ \log p(w_j|w_i) = {\bf v_i^T u_j} - \log{\sum_{a=1}^{V} \exp({\bf v_i^T u_a})} \tag{3-6} \]
而式3-6对\(\bf v_i\)梯度为 \[ \begin{aligned} \frac{\partial \text{log}\, P(w_j \mid w_i)}{\partial \bf{v}_i} &= {\bf u_j} - \frac{\sum_{b=1}^{V} \exp({\bf v_i^T u_b}){\bf u_b}}{\sum_{a=1}^{V} \exp({\bf v_i^T u_a})}\\ &= {\bf u_j} - \sum_{b=1}^{V}\frac{\exp({\bf v_i^T u_b})}{\sum_{a=1}^{V}\exp({\bf v_i^T u_a})} {\bf u_b} \\ &= {\bf u_j} - \sum_{b=1}^{V} P(w_b \mid w_i) {\bf u_b} \end{aligned}\tag{3-7} \] 同理对\(u_j\)的梯度为 \[ \begin{aligned} \frac{\partial \text{log}\, P(w_j \mid w_i)}{\partial \bf{u}_j} &= {\bf v_i} - \frac{\exp({\bf v_i^T u_j}){\bf v_i}}{\sum_{a=1}^{V} \exp({\bf v_i^T u_a})}\\ &= {\bf v_i} - P(w_j \mid w_i) {\bf v_i} \end{aligned}\tag{3-8} \]
3-5的式子其实也可以看成是交叉熵损失,标签y为one-hot的结果,则 \[ L({\bf W}) = - \sum_{-m \leq j \leq m,\ j \neq 0} \sum_{a=1}^V y_a^{(i+j)} \log P(w^{(i+j)} \mid w^{(i)})\tag{3-9} \] 但每个\(\bf y^{(i+j)}\)中只有一个为1,其余的为0,因此最后就和3-5等价了。
CBOW 模型
CBOW(continuous bag-of-word)即连续词袋模型,即用一个中心词前后距离d内的背景词来预测该中心词出现的概率。
为了方便理解,再把上面的例子的条件概率抄下来: \[ P(\textrm{fox} \mid\textrm{quick},\textrm{brown},\textrm{jumps},\textrm{over}) \] 更一般的,给定长度为T的文本序列,设窗口大小为m, 可以用似然函数表示为: \[ \prod_{t=1}^{T} P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)}) \tag{4-1} \] 同样的,我们先来看看网络结构,然后再讨论P的形式。
CBOW模型可以用如下的一层神经网络表示:
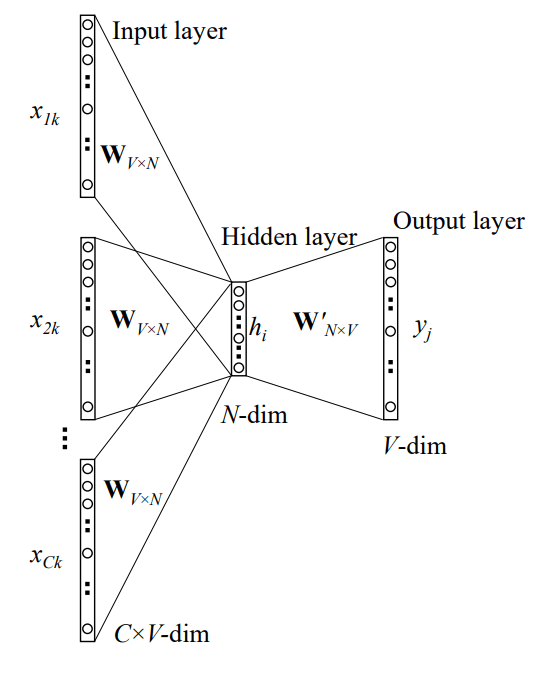
和Skip-gram类似,首先对背景词都进行one-hot处理,每个背景词都得到对应的one-hot向量\(\bf x\),然后每个背景词的向量\(\bf x\)都和矩阵\(\bf W\)相乘,然后求和取平均,公式如下: \[ {\bf \bar v} = \frac{1}{C} \sum_{i=1}^{C}{\bf W^T x^{(i)}} = \frac{1}{C} \sum_{i=1}^{C}{\bf v_{i}}\tag{4-2} \] 这里的C等于2m,即我们滑动窗口的两倍。
从隐层到输出层和之前的类似,和另一个矩阵\(\bf W'\)相乘,这里假设中心词下标为j,有\(t_j = {\bf v^T u_j }\),其中\({\bf u_j}\)为\(\bf W'\)的第j列(\(N \times 1\)),结果得到一个数\(u_k\)。然后放入Softmax进行概率归一化: \[ p(w_j|w_1,\dots,w_C) = y_j = \frac{\exp({\bf {\bar v}^T u_j })}{\sum_{k = 1}^{V}\exp({\bf {\bar v}^T u_k})}\tag{4-3} \]
训练
和Skip-gram类似,最大化似然等价于最小化负的对数似然: \[ \mathcal{L} =- \sum_{t=1}^{T} \log P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)})\tag{4-4} \]
4-3取对数得: \[ \log P(w_j|w_1,\dots,w_C) = {\bf {\bar v}^T u_j } - \log{\sum_{k = 1}^{V}\exp({\bf{\bar v}^T u_k}})\tag{4-3} \] 4-3对中心词向量\(\bf u_j\)求导得: \[ \begin{aligned} \frac{\partial \text{log}\, P}{\partial \bf{u}_j} &= {\bf {\bar v}} - \frac{\exp({\bf {\bar v}^T u_j}){\bf {\bar v}}}{\sum_{a=1}^{V} \exp({\bf {\bar v}^T u_a})}\\ &= {\bf {\bar v}} - P(w_j|w_1,\dots,w_C) {\bf {\bar v}} \end{aligned}\tag{4-4} \] 对于任意的背景词向量\(\bf v_i\),4-3对其求导有: \[ \begin{aligned} \frac{\partial \text{log}\, P}{\partial \bf{v}_i} &= \frac{1}{C} {\bf u_j} - \frac{\sum_{b=1}^{V}\exp({\bf {\bar v}^T u_b})\frac{1}{C} {\bf u_b} }{\sum_{a=1}^{V} \exp({\bf {\bar v}^T u_a})}\\ &= \frac{1}{C} \left({\bf u_j} - \sum_{b=1}^VP(w_b|w_1,\dots,w_C) {\bf u_b} \right) \end{aligned}\tag{4-5} \]
加速计算
可以看出计算Softmax的时候,需要计算求和项,(在计算梯度的时候也要计算求和项),而计算求和项的复杂度是\(O(V)\)级的,即和词库大小挂钩,对于较大的词库,开销会比较大。
为此,有两种技术来加速这个过程。下面以Skip-Gram模型为例来讲解两种优化的技术。
负采样 negative sampling
负采样(negative sampling)其实是将原来的多分类训练方法转化为二分类,即给定\(w_c\)和\(w_i\)两个词,\(w_i\)在\(w_c\)窗口内的概率。
如何训练呢?我们需要进行采样得到正例和负例。所谓的正例和负例就是神经网络输出的结果分别为1和0。
以之前的The quick brown fox jumps over the lazy dog例子来说,
- 正例:即中心词\(w_c\)和窗口范围内每个背景词\(w_i\)分别组成的pair就是正例。(和之前的一样)
- 负例:用相同的中心词\(w_c\),然后在词库中随机抽取k个词,中心词和这k个词分别组成pair,得到的k个pair都标记为负例。这里的k一般取5~20。这里有个小细节,比如我的中心词是fox,窗口大小为2,但是我从词库中抽取的词是brown,在该句子中其实是在fox前面的,但是仍然算作负例。
还有另外一个细节是负样本的选择,考虑我们在词库中进行随机的取词,我们希望取词组成的样本对比较具有代表性,这样训练出的效果会比较好,考虑两种简单的取词方案:
- 如果用均等的概率选择的话,其实对于英文的文本是没有代表性的。
- 如果用出现的频率来取词,像"the"这些stop words的采样得到的概率会很大,但是("fox", "the") 并不能告诉我们很多的信息,因为the这个单词在很多上下文都出现过。
因此,word2vec采用了一种tradeoff的方式,即和频率不完全挂钩: \[ P(w_i) = \frac{ {f(w_i)}^{3/4} }{\sum_{j=0}^{n}\left( {f(w_j)}^{3/4} \right) }\tag{4-6} \] 其中,\(f(w_i)\)是单词\(w_i\)的频率,\(3/4\)是经验值。
负采样的公式表示
上面提到,负采样将原来的多分类转化为了二分类问题,因此避免了Softmax分母求和项的计算。下面用公式形式化的说明这一过程。(主要参考《动手学深度学习》的内容)
负采样考虑一对词 \(w_c\) 和 \(w_o\) 是不是可能组成中心词和背景词对,即 \(w_o\) 是否可能出现在 \(w_c\) 的背景窗口里。我们假设会出现在窗口的概率为: \[ P(D=1\mid w_c, w_o) = \sigma({\bf v_c^T u_o}) = \frac{1}{1+e^{-{\bf v_c^T u_o}}}\tag{4-7} \]
给定一个长度为T的文本序列,窗口大小为m,则我们可以用极大似然估计来学习: \[ \prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} \mathbb{P}(D=1\mid w^{(t)}, w^{(t+j)})\tag{4-8} \] 但这个模型里只有正例样本,我们可以让所有词向量相等且值为无穷大,这样上面概率等于最大值 1,我们可以加入负例样本来使得目标函数更有意义。在负采样中,我们为每个中心词和背景词对根据分布 \(P(w)\)采样 K 个没有出现在背景窗口的的词,它们被称为噪音词,并最大化它们不出现的概率。而分布\(P(w)\)就是上面的公式4-6。
这样,我们得到下面目标函数: \[ \prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} \left(\mathbb{P}(D=1\mid w^{(t)}, w^{(t+j)})\prod_{k=1,\ w_k \sim \mathbb{P}(w)}^K \mathbb{P}(D=0\mid w^{(t)}, w_k)\right)\tag{4-9} \] 记词\(w^{(t)}\)的所因为\(i_t\),则最大化上面目标函数等价于最小化它的负对数值: \[ - \sum_{t=1}^{T} \sum_{-m \leq j \leq m,\ j \neq 0} \left(\log\, \sigma(\boldsymbol{v_{i_{t}}}^\top \boldsymbol{u_{i_{t+j}}}) + \sum_{k=1,\ w_k \sim \mathbb{P}(w)}^K \log\left(1-\sigma(\boldsymbol{v_{i_t}}^\top \boldsymbol{u_{k}})\right)\right)\tag{4-9} \]
层次 Softmax
层次Softmax(Hierarchical Softmax )是另外一种加速训练的方法,它相对负采样的方法来说比较复杂。
层次Softmax采用的是Huffman树,首先统计语料中词语的词频,然后根据词频来构建Huffman树。
下图是一个例子,树的根节点可以理解为输入词的词向量,每个叶子节点代表着词典中的一个单词,中间节点仅仅是辅助作用,没什么实际的含义。
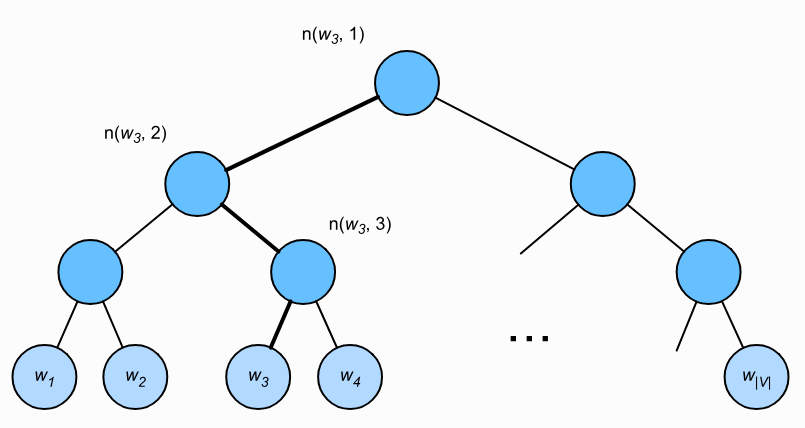
假设\(L(W)\)为二叉树的根节点到词\(w\)的叶子节点的路径上的节点数(包括根和叶子节点),设\(n(w,j)\)为该路径上第\(j\)个节点,并设该节点的背景词向量为\(\mathbf{u}_{n(w,j)}\)。以上图为例,\(L(w_3) = 4\),层次Softmax将skip-gram模型中的条件概率近似表示为: \[ \mathbb{P}(w_o \mid w_c) = \prod_{j=1}^{L(w_o)-1} \sigma\left( [\![ n(w_o, j+1) = \text{leftChild}(n(w_o,j)) ]\!] \cdot \mathbf{v}_c^\top \mathbf{u}_{n(w_o,j)} \right)\tag{4-10} \] 其中,\(\sigma\)表示sigmoid函数,\([\![ n(w_o, j+1) = \text{leftChild}(n(w_o,j)) ]\!]\)表示的是如果第j + 1个结点是第j个结点的左儿子的话,则值为1,否则为-1。这相当于每次决定结点向左还是向右走是一个二分类问题。
举个例子,计算给定中心词\(w_c\)后,\(w_3\)的条件概率,根据式4-10,要将路径上的概率练成起来: \[ \mathbb{P}(w_3 \mid w_c) = \sigma(\mathbf{v}_c^\top \mathbf{u}_{n(w_3,1)}) \cdot \sigma(-\mathbf{v}_c^\top \mathbf{u}_{n(w_3,2)}) \cdot \sigma(\mathbf{v}_c^\top \mathbf{u}_{n(w_3,3)} ) \] 可以看出,这开销和路径的长度是有很大的关系的, 因此实际中采用的是Huffman树,进行不等长编码,频率越高的词越接近根节点,这使计算量有所降低。这样加快了速度。
此外,由于输出层不使用one-hot来表示,Softmax回归就不需要对那么多0(也即负样本)进行拟合,仅仅只需要拟合输出值在Huffman树中的一条路径。假设词表大小为V,一条路径上节点的个数可以用\(O(log_2|V|)\)来估计,就是说只需要拟合\(O(log_2|V|)\)次,这给计算量带来了指数级的减少。
注意到\(\sigma(x) + \sigma(-x) = 1\),给定中心词\(w_c\)生成词典中任一词的条件概率之和为1这一条件也满足: \[ \sum_{w \in \mathcal{V}} \mathbb{P}(w \mid w_c) = 1 \]
欠采样 subsample
- 负采样的方式通过考虑同时含有正例样本和负例样本的相互独立事件来构造损失函数,其训练中每一步的梯度计算开销与采样的负例个数线性相关.
- 层次Softmax使用了Huffman树,并根据根节点到叶子结点的路径来构造损失函数,其训练中每一步的梯度计算开销与词典大小对数相关.
其实除了上面提到的负采样和层次Softmax来提升训练速度外,训练过程中还有欠采样(subsample)的方式。
一些词如"the"等stop words,这些词并不包含多少语义,而且出现的频率特别高,如果不加处理会影响词向量的效果。欠采样就是为了应对这种现象,它的主要思想是对每个词都计算一个采样概率,根据概率值来判断一个词是否应该保留。在语料库或者说训练集中的每个词,如果计算出该词不被保留,那么我们就将该词删除。
概率计算方法为: \[ p(word) = \left(\sqrt{\frac{f(word)}{0.001}+1}\right) \cdot\frac{0.001}{f(word)} \] 其中f(word)表示word出现的概率,0.001为默认值。
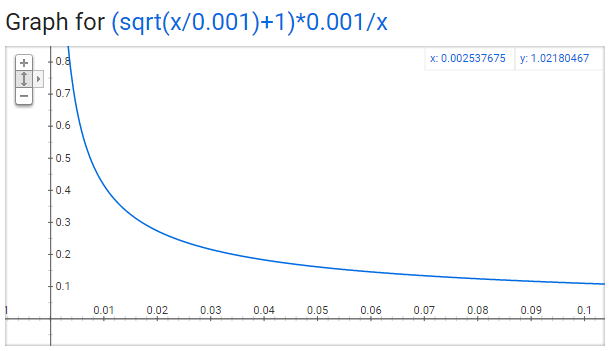
可以看出,词语出现的概率越高,其被采样到的概率就越低。这里有一点IDF的味道,不同的是IDF是为了降低词的特征权重,欠采样是为了降低词的采样概率。
CBOW 和 Skip-gram对比
上面提到的word2vec有两种计算方法,CBOW和Skip-gram,那么他们谁更好呢?
从速度上说,CBOW训练更快。考虑窗口大小为2,那么CBOW需要计算的是4个one-hot向量分别乘以\(\bf W\)矩阵,然后计算均值。实际上我们可以直接选取\(\bf W^T\)的列出来,然后计算均值。接着计算和\(\bf W\)矩阵乘积,最后反向传播,这样总开销为1次前向传播和1次反向传播。而Skip-gram则需要分别计算4个词的正向传播和反向传播,和窗口大小成正比。所以说CBOW模型速度更快。
但是Skip-gram对于低频词更准确。Stack exchange有一个很好的解释:
In CBOW the vectors from the context words are averaged before predicting the center word. In skip-gram there is no averaging of embedding vectors. It seems like the model can learn better representations for the rare words when their vectors are not averaged with the other context words in the process of making the predictions.
As we know, CBOW is learning to predict the word by the context. Or maximize the probability of the target word by looking at the context. And this happens to be a problem for rare words. For example, given the context
yesterday was really [...] dayCBOW model will tell you that most probably the word isbeautifulornice. Words likedelightfulwill get much less attention of the model, because it is designed to predict the most probable word. Rare words will be smoothed over a lot of examples with more frequent words.On the other hand, the skip-gram is designed to predict the context. Given the word
delightfulit must understand it and tell us, that there is huge probability, the context isyesterday was really [...] day, or some other relevant context. With skip-gram the worddelightfulwill not try to compete with wordbeautifulbut instead,delightful+contextpairs will be treated as new observations. Because of this, skip-gram will need more data so it will learn to understand even rare words.from https://stats.stackexchange.com/a/261440
相对而言,skip-gram用得更多一点。
关于在大数据集上用哪个模型stack overflow上有帖子讨论:word2vec: CBOW & skip-gram performance wrt training dataset size
参考资料
- Word2Vec Tutorial - The Skip-Gram Model
- 词嵌入(word2vec)
- Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]//Advances in neural information processing systems. 2013: 3111-3119.
- 漫谈Word2vec之skip-gram模型
- Meyer D. How exactly does word2vec work?[J]. 2016.
- DeepLearning.ai 吴恩达 第五课第二周, 自然语言处理与词嵌入

